StretchSense Partners with Movella to Deliver Indie Program
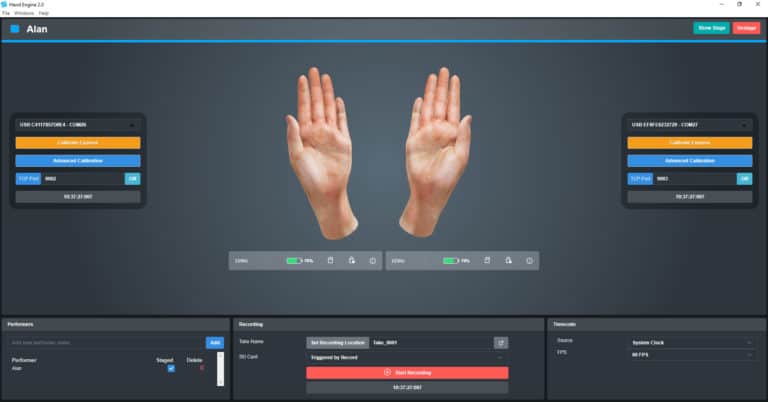
The StretchSense Pro Studio Glove for Xsens delivers professional-grade motion capture tailored for independent creators. With Hand Engine software now seamlessly integrated with Unity, Unreal Engine, and Movella’s MVN software, creators can express themselves vividly through their hands. Priced at